14.3.100 SST, SSR, and SSE

Following are chest size and weight data for 8 randomly selected bears. Here, x denotes chest size, in inches, and y denotes weight, in pounds. Use the information to do parts (a) through (d).

\(\sum x = 396, \sum y = 2362, \sum xy = 118330, \sum x^2 = 19870\)

Compute SST, SSR, and SSE, using the formulas, .

First we need to get the data from the question. (We can import it from Excel)

x<- c(55, 44, 46, 58, 40, 54, 52, 47)
y<- c(325, 253, 263, 340, 251, 315, 310, 305)

From formula sheet

\(S_{xx}=\sum(x_i-\bar{x})^2=\sum x_i^2-(\sum x_i)^2/n\)

\(S_{xy}=\sum(x_i-\bar{x})(y_i-\bar{y})=\sum x_iy_i-(\sum x_i)(\sum y_i)/n\)

\(S_{yy}=\sum(y_i-\bar{y})^2=\sum y_i^2-(\sum y_i)^2/n\)

Total sum of squares: \(SST =\sum(y_i-\bar{y})^2 = S_{yy}\)

Regression sum of squares: \(SSR=\sum(\hat{y_i}-\bar{y})^2=S_{xy}^2/S_{xx}\)

Error sum of squares: \(SSE=\sum (y_i-\hat{y_i})^2=S_{yy} - S_{xy}^2/S_{xx}\)

Regression identity: \(SST = SSR + SSE\)

Coefficient of determination: \(r^2=\frac{SSR}{SST}\)

Linear correlation coefficient: \(r=\frac{\frac{1}{n-1}\sum(x_i-\bar{x})(y_i-\bar{y})}{s_xs_y}\) or \(r=\frac{S_{xy}}{\sqrt{S_{xx}S_{yy}}}\)

Names of variables

\(S_{xx}: Sxx\)

\(S_{xy}: Sxy\)

\(S_{yy}: Syy\)

First approach, we find SST, SSR, SSE without finding \(\bar x, \bar y\)

n = length(x)

We have the same dataset from the question.

Find \(S_{xy}, S_{xx}, S_{yy}\)

Syy = sum(y*y) - sum(y)^2/n
Sxx = sum(x*x) - sum(x)^2/n
Sxy = sum(x*y) - sum(x) * sum(y) /n

Sxx

## [1] 268

Sxy

## [1] 1411

Syy

## [1] 8373.5

Find SST

SST = Syy
SST

## [1] 8373.5

Round to two decimal places

round(SST,2)

## [1] 8373.5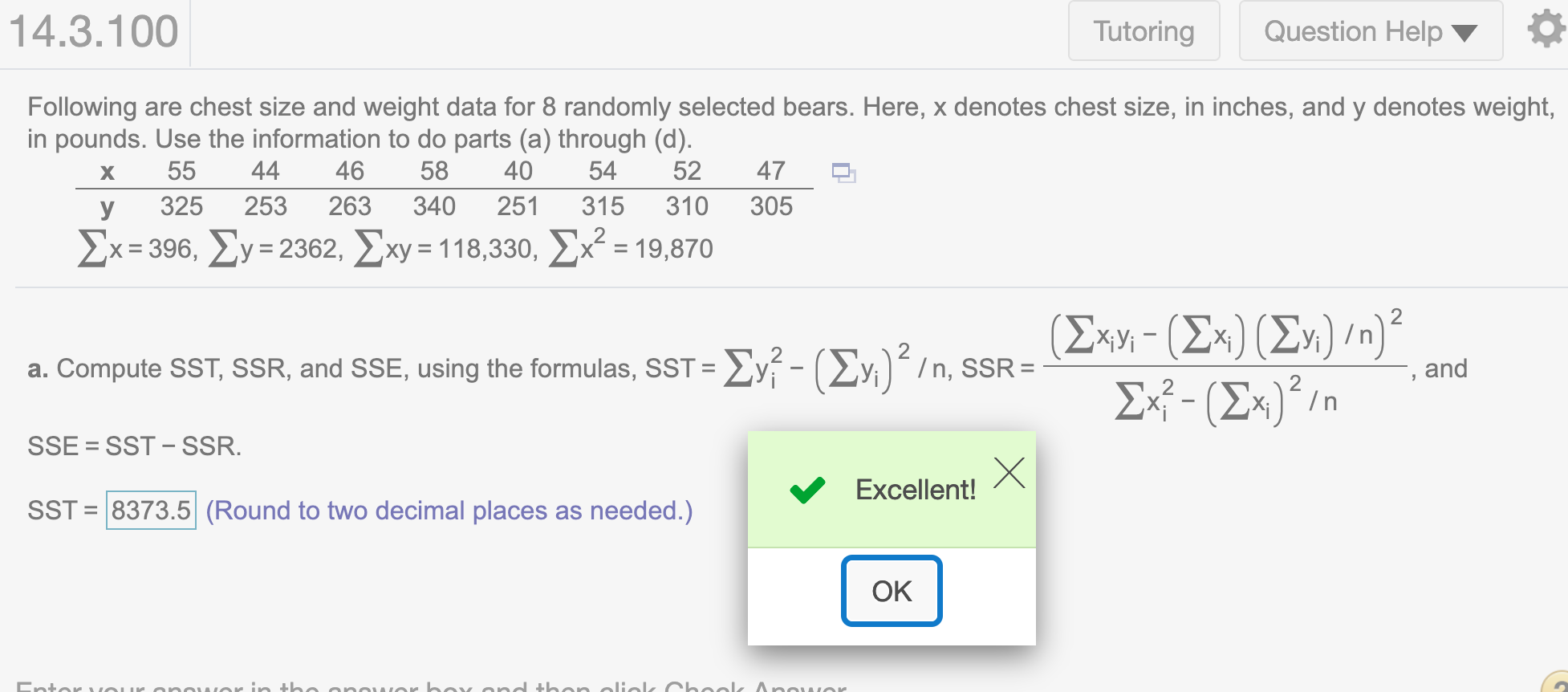

Find SSR

SSR = Sxy^2/Sxx
SSR

## [1] 7428.81

Round to two decimal places

round(SSR,2)

## [1] 7428.81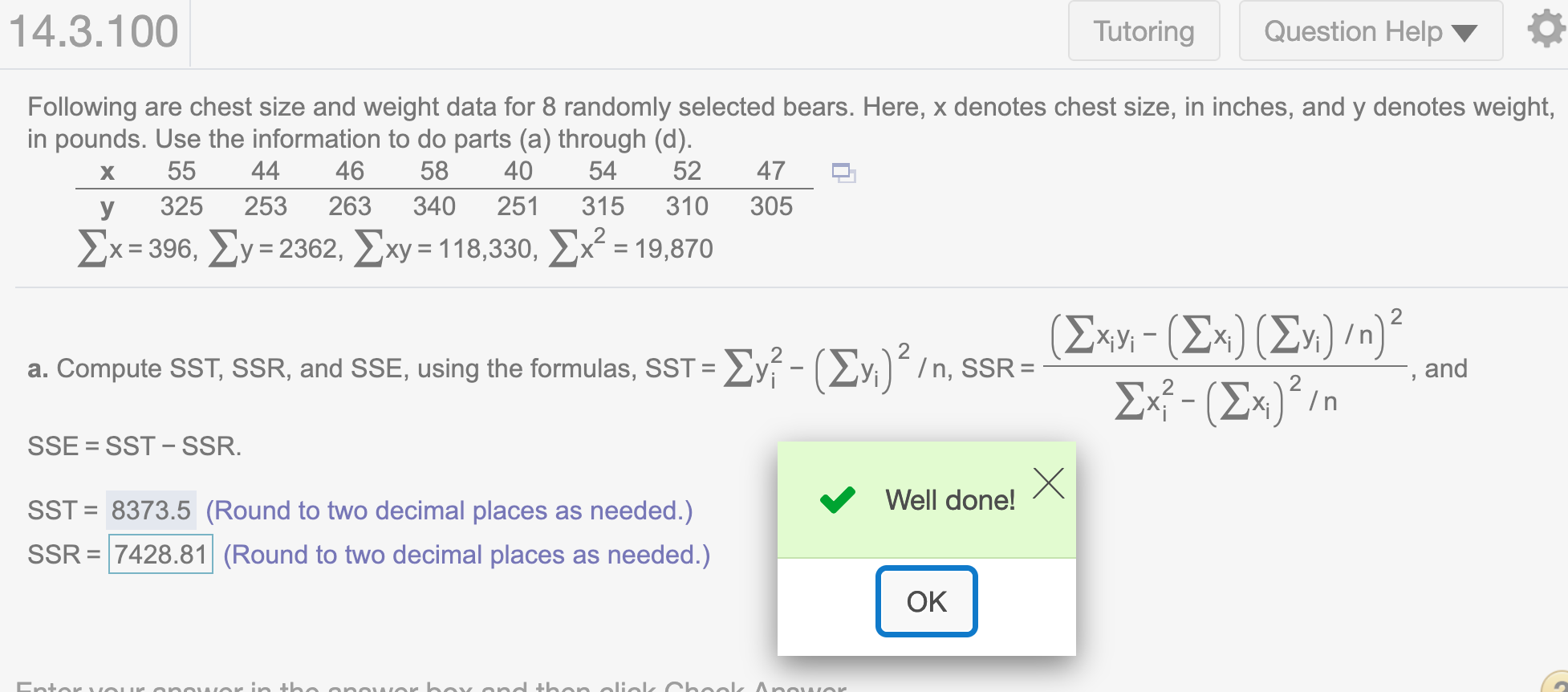

Find SSE

SSE = Syy - Sxy^2/Sxx
SSE

## [1] 944.6903

Round to two decimal places

round(SSE,2)

## [1] 944.69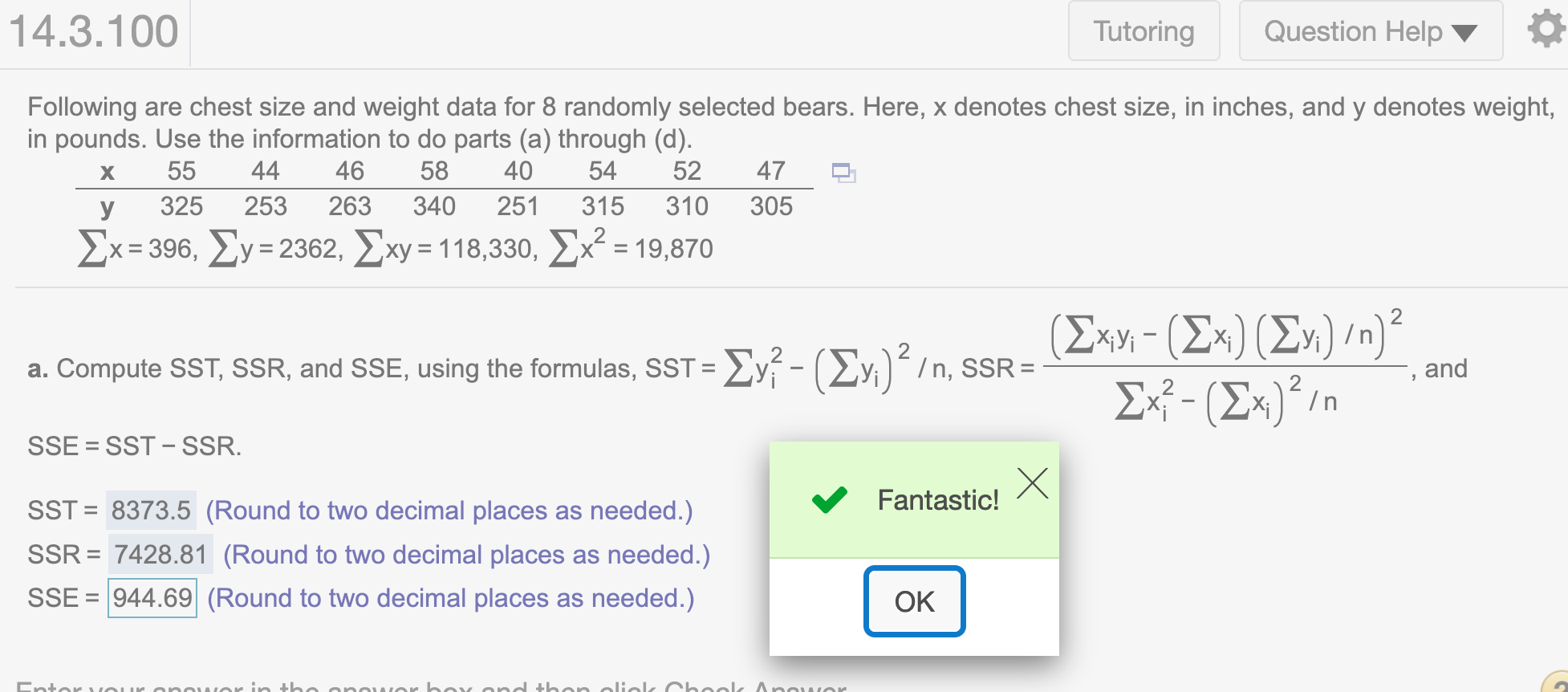

Check if SSE + SSR = SST

SSE + SSR == SST

## [1] TRUE

Second approach finding SST, SSR, SSE using \(\bar x, \bar y\)

Sxx = sum((x-mean(x))^2)
Sxy = sum((x-mean(x))*(y-mean(y)))
Syy = sum((y-mean(y))^2)

Sxx

## [1] 268

Sxy

## [1] 1411

Syy

## [1] 8373.5

(b) Compute the coefficient of determination, \(r^2\)

First approach: using the formula

Linear correlation coefficient

r = Sxy/sqrt(Sxx*Syy)
r

## [1] 0.9419028

Coefficient of determination \(r^2\)

r^2

## [1] 0.887181

Round to four decimal places

round(r^2, 4)

## [1] 0.8872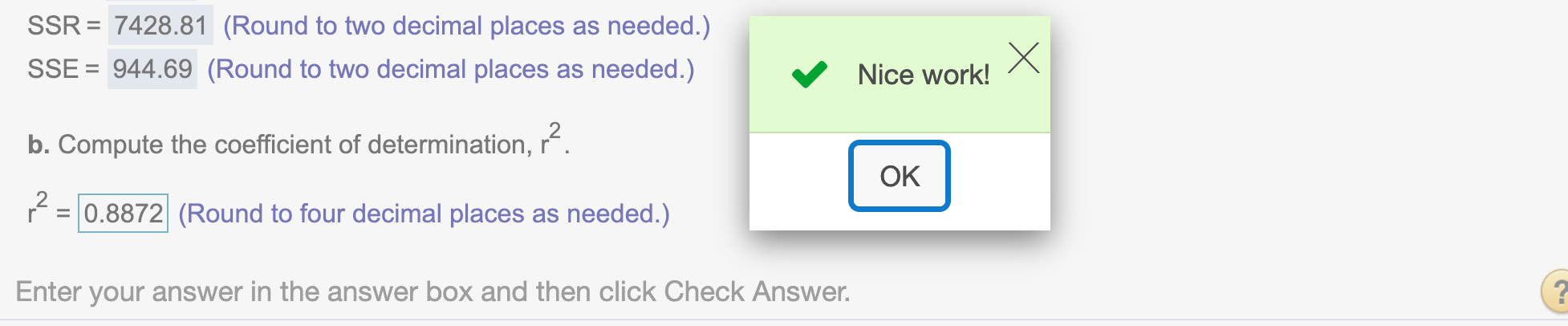

Second approach: using summary() in R

Multiple R-squared = coefficient of determination

summary(lm(y~x))

## 
## Call:
## lm(formula = y ~ x)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -13.8228  -6.2799   0.3955   2.6325  22.9123 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  34.6362    38.1993   0.907 0.399502    
## x             5.2649     0.7665   6.869 0.000469 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 12.55 on 6 degrees of freedom
## Multiple R-squared:  0.8872, Adjusted R-squared:  0.8684 
## F-statistic: 47.18 on 1 and 6 DF,  p-value: 0.0004691

Third approach: using cor() in R To find r, we run

cor(x,y)

## [1] 0.9419028

To find \(r^2\), we run

cor(x,y)^2

## [1] 0.887181

Round to 4 decimal places

round(cor(x,y)^2, 4)

## [1] 0.8872

(c) Determine the percentage of variation in the observed values of the response variable explained by the regression, and interpret your answer.

Show percentage value of \(r^2\)

round(cor(x,y)^2, 4) * 100

## [1] 88.72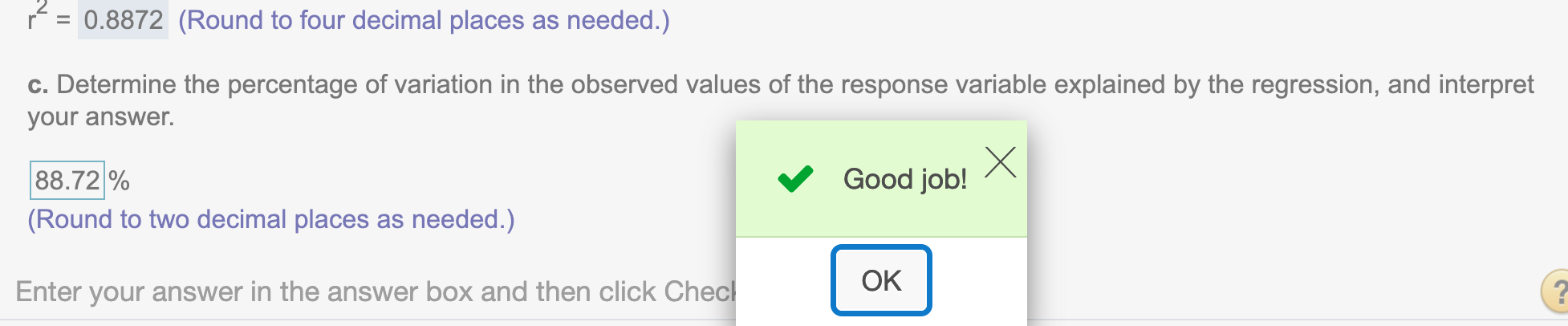

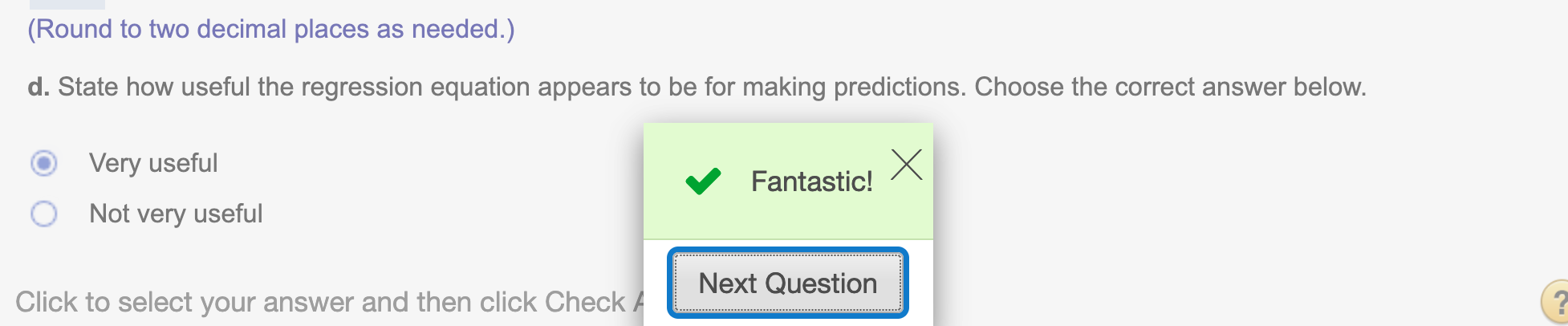
(d) State how useful the regression equation appears to be for making predictions. Choose the correct answer below.

Since the \(r^2\) value is close to 1, it is very useful to use regression equation

Hope that helps!

14.3.100 SST, SSR, and​ SSE

14.3.100 SST, SSR, and SSE