14.3.97 SST, SSR, and​ SSE

Use the table and the given regression equation to answer parts​ (a)-(e). \(\hat{y}=7.7 - 1.5x\)

---

Compute​ SST, SSR, and​ SSE, using the​ formulas, .

First we need to get the data from the question. (We can import it from Excel)

x<- c(0, 2, 2, 5, 6)
y<- c(8, 10,  0, -4,  2)

---

From formula sheet

\(S_{xx}=\sum(x_i-\bar{x})^2=\sum x_i^2-(\sum x_i)^2/n\)

\(S_{xy}=\sum(x_i-\bar{x})(y_i-\bar{y})=\sum x_iy_i-(\sum x_i)(\sum y_i)/n\)

\(S_{yy}=\sum(y_i-\bar{y})^2=\sum y_i^2-(\sum y_i)^2/n\)

---

Total sum of squares: \(SST =\sum(y_i-\bar{y})^2 = S_{yy}\)

Regression sum of squares: \(SSR=\sum(\hat{y_i}-\bar{y})^2=S_{xy}^2/S_{xx}\)

Error sum of squares: \(SSE=\sum (y_i-\hat{y_i})^2=S_{yy} - S_{xy}^2/S_{xx}\)

Regression identity: \(SST = SSR + SSE\)

Coefficient of determination: \(r^2=\frac{SSR}{SST}\)

Linear correlation coefficient: \(r=\frac{\frac{1}{n-1}\sum(x_i-\bar{x})(y_i-\bar{y})}{s_xs_y}\) or \(r=\frac{S_{xy}}{\sqrt{S_{xx}S_{yy}}}\)

---

Names of variables

\(S_{xx}: Sxx\)

\(S_{xy}: Sxy\)

\(S_{yy}: Syy\)

Compute the three sums of​ squares, SST,​ SSR, and​ SSE, using the defining formulas.

Since the quesiton gives linear regression line, we will find SST, SSR, and SSE by using the first formula.

We could find SST, SSR, and SSE by using the same approach in question 14.3.100 without linear regression line. We can consider that approach is for double checking purpose.

To compute \(\hat{y}\)

yh = 7.7 - 1.5 * x

Find SST

SST = sum( (y-mean(y))^2 )
SST

## [1] 132.8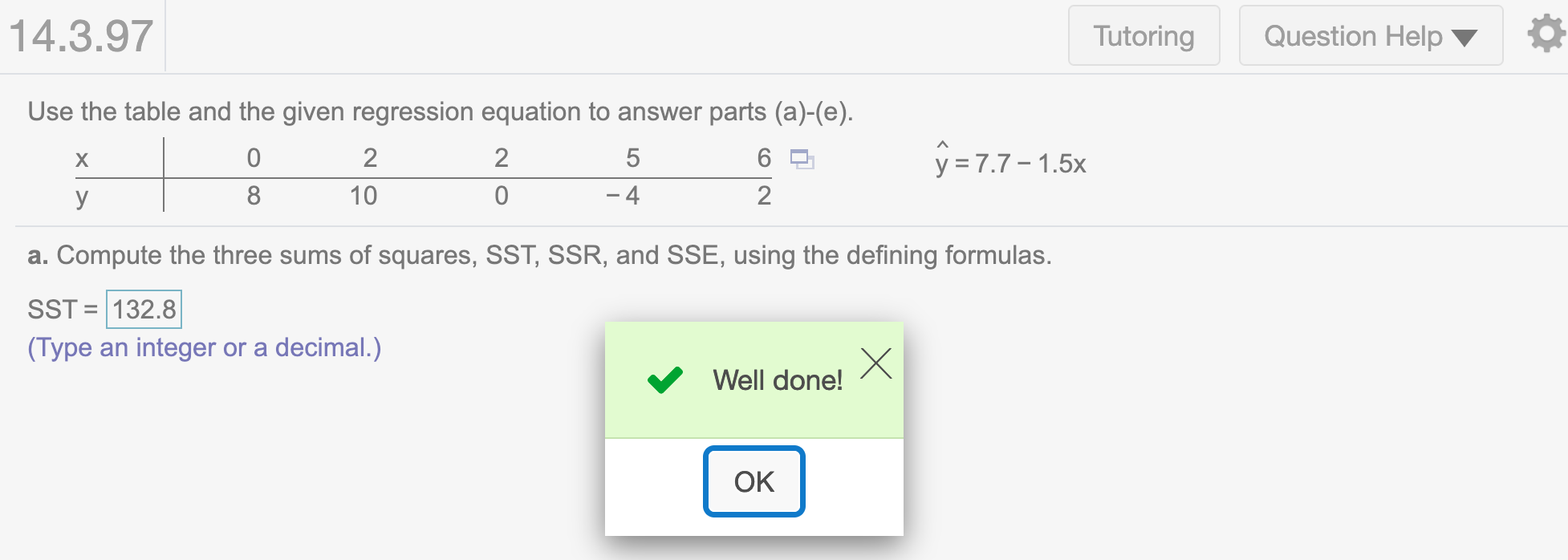

---

---

Find SSR

SSR = sum( (yh-mean(y))^2 )
SSR

## [1] 54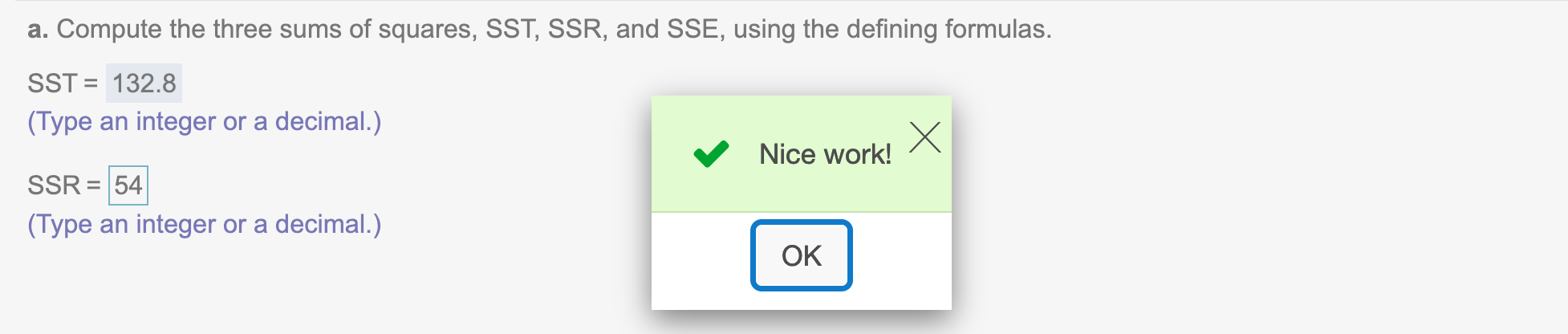

---

---

Find SSE

SSE = sum( (y-yh)^2 )
SSE

## [1] 78.8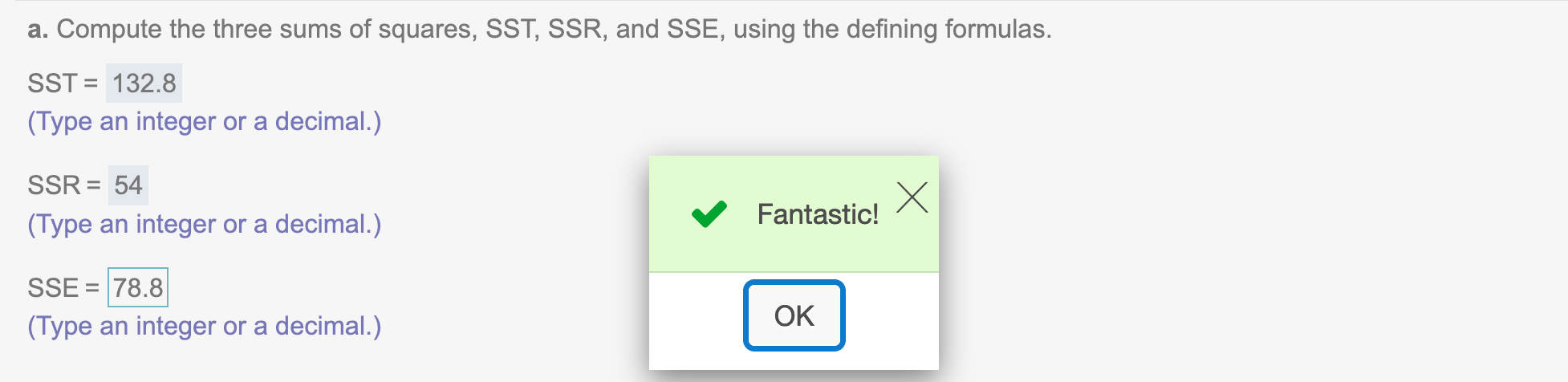

---

---

(b). Verify the regression​ identity, SST​ = SSR​ + SSE. Is this statement​ correct?

SSE + SSR == SST

## [1] TRUE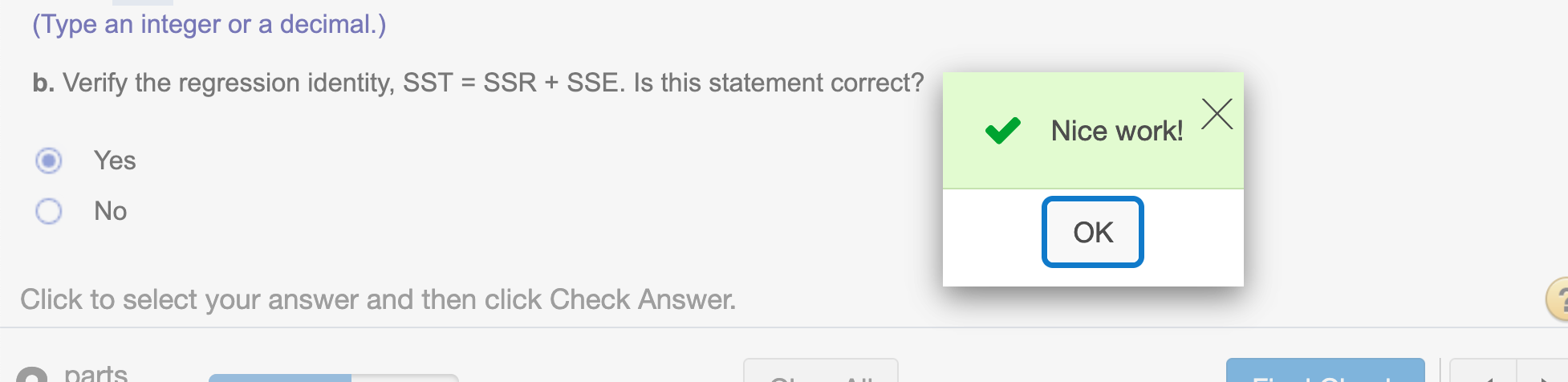

---

---

(c). Determine the value of \(r^2\)​, the coefficient of determination. Second approach: using summary() in R

We can use the formula \(r^2=\frac{SSR}{SST}\) and round to four decimal places

round(SSR/SST, 4)

## [1] 0.4066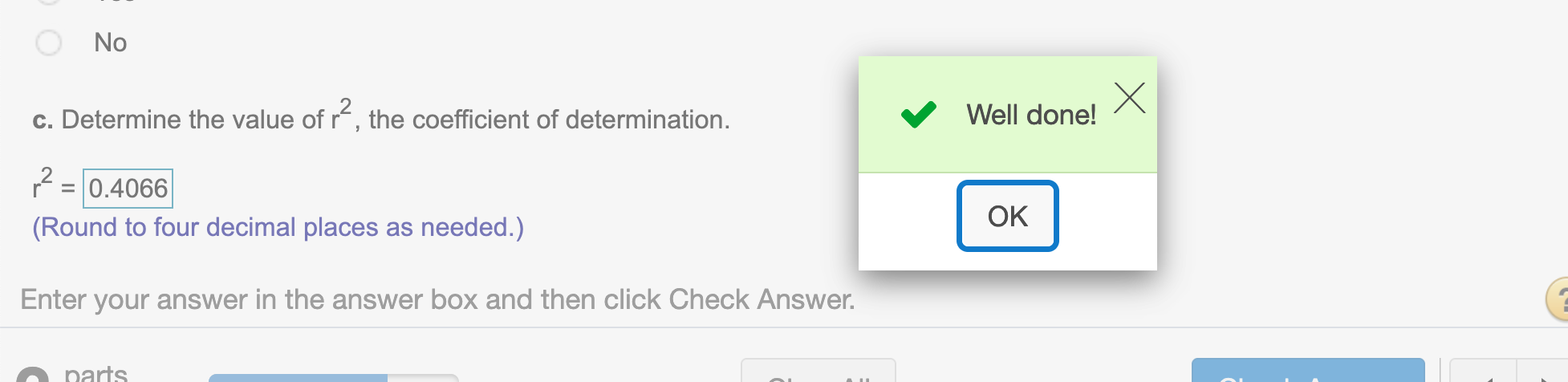

---

---

(d) Determine the percentage of variation in the observed values of the response variable that is explained by the regression.

Show percentage value of \(r^2\)

round(SSR/SST, 4) * 100

## [1] 40.66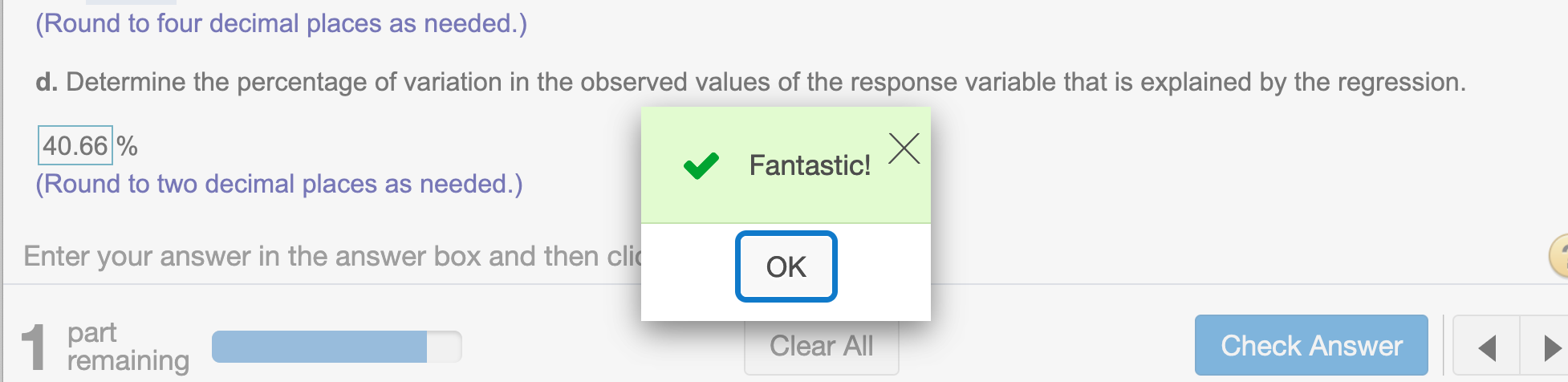

---

---

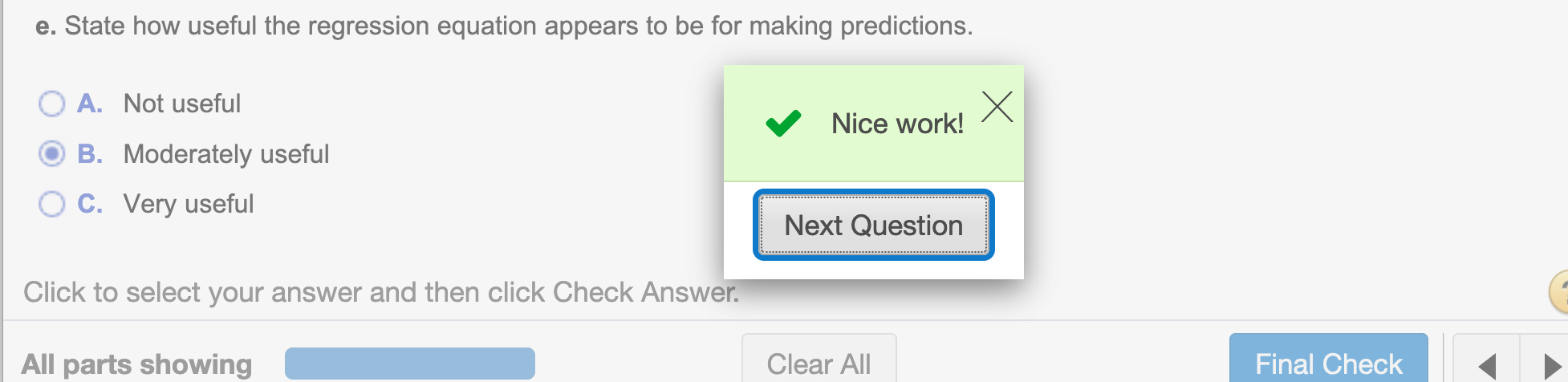
(e) State how useful the regression equation appears to be for making predictions.

Since the \(r^2\) value is close to .5, it is moderately useful to use regression equation

---

---

Hope that helps!