9.4.77 left-tailed z-test without data

A sample​ mean, sample​ size, and population standard deviation are provided below. Use the​ one-mean z-test to perform the required hypothesis test at the 1% significance level.

\(\bar x\) = 17, n =34, \(\sigma\) = 10, \(H_0: \mu =22, H_a: \mu < 22\)

The test statistic is z =

First, we need to get the data the question

x = 17
n = 34
sigma = 10
mu = 22

---

To get the test statistic z we use the formular \(z = (\bar x-\mu)/(\sigma/\sqrt{n})\), we run

z = (x-mu)/(sigma/sqrt(n))
z

## [1] -2.915476

Round the answer to two decimal places

round(z,2)

## [1] -2.92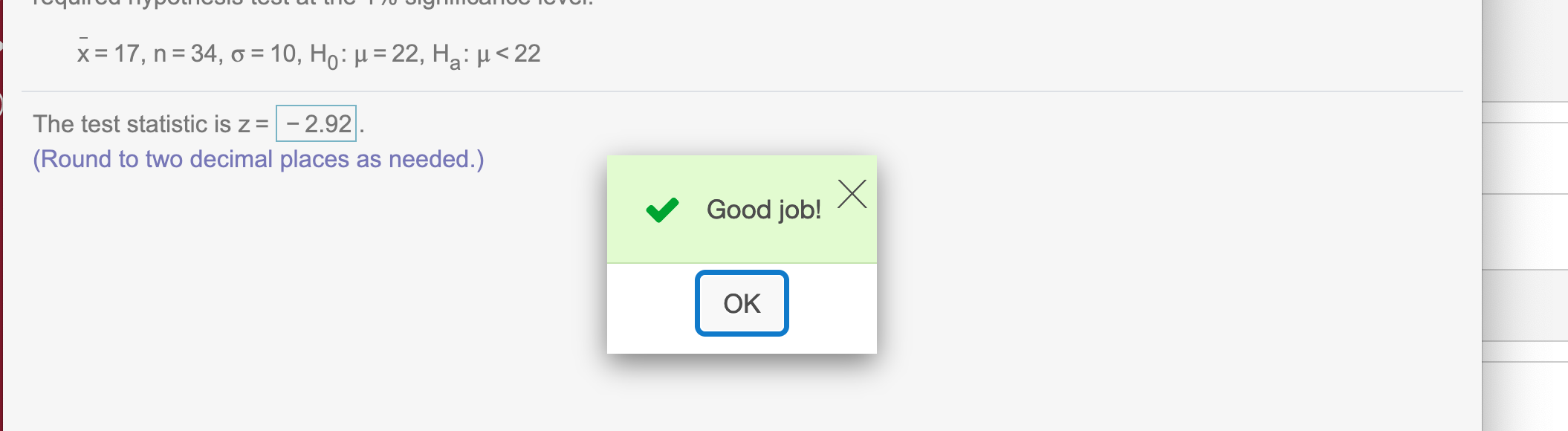

---

---

(b) Identify the critical​ value(s). Select the correct choice below and fill in the answer box within your choice.​(Round to two decimal places as​ needed.).

First, this is a left tail test since \(H_a: \mu < 22\), we have the negative critical value which is on the left of the graph.

Since the significance level is 1%, we can use qnorm() to get the z value

qnorm(.01)

## [1] -2.326348

---

Round to two decimal places

round(qnorm(.01), 2)

## [1] -2.33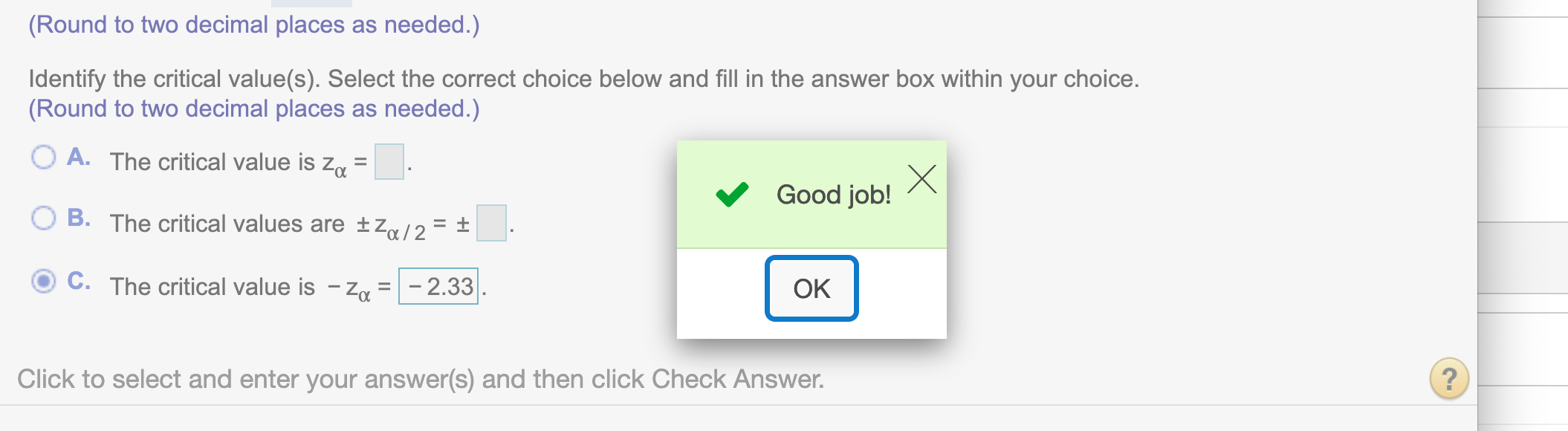

---

---

Since our test statistic z = -2.92 < our critical value \(z_{\alpha}\) = -2.33, out test statistic lies in the rejected region. So we have enough evidence to reject null hypothesis.

---

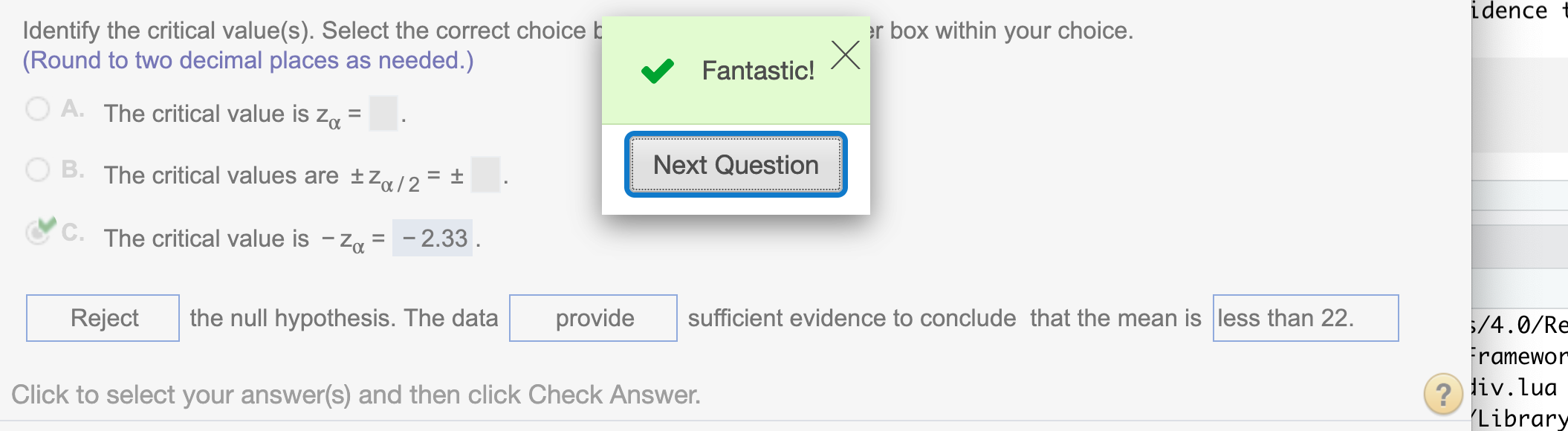
Hope that helps!