10.2.51 pooled t-test with data

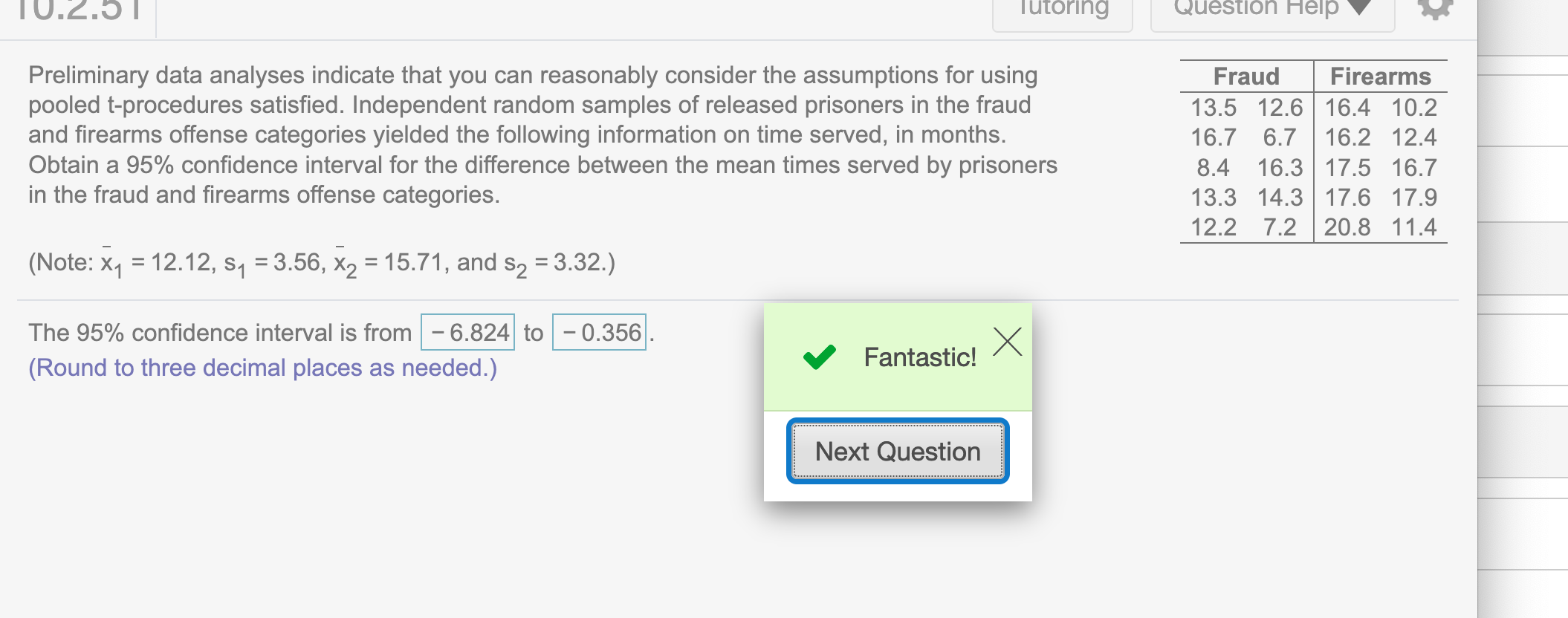
Preliminary data analyses indicate that you can reasonably consider the assumptions for using pooled​ t-procedures satisfied. Independent random samples of released prisoners in the fraud and firearms offense categories yielded the following information on time​ served, in months. Obtain a 95 % confidence interval for the difference between the mean times served by prisoners in the fraud and firearms offense categories. (Note: \(\bar x_1=12.12, s_1=3.56, \bar x_2=15.71, s_2=3.32\))

The 95% confidence interval is from … to …

First, we need to get the data from the question

fraud <- c(13.5, 12.6, 16.7, 6.7, 8.4, 16.3, 13.3, 14.3, 12.2, 7.2)
firearms <- c(16.4, 10.2, 16.2, 12.4, 17.5, 16.7, 17.6, 17.9, 20.8, 11.4)

The note means that these data are optional to know. In the case that the question does not provide these data, we could find sample mean, sample standard deviation, and size by running

Round to two decimal places

round(mean(fraud), 2)

## [1] 12.12

round(sd(fraud), 2)

## [1] 3.56

length(fraud)

## [1] 10

round(mean(firearms), 2)

## [1] 15.71

round(sd(firearms),2)

## [1] 3.32

length(firearms)

## [1] 10

We have the same data set with the note from the question, we could use the same approach in question 10.2.41 to find confidence interval

or we could use t.test() function in R to find confidence interval

Since this is a pooled t-test, we specify var.equal = TRUE

t.test(fraud, firearms, conf.level=.95, var.equal = TRUE)

## 
##  Two Sample t-test
## 
## data:  fraud and firearms
## t = -2.3324, df = 18, p-value = 0.03149
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -6.8237597 -0.3562403
## sample estimates:
## mean of x mean of y 
##     12.12     15.71

To have 3 decimal places, we can use print() command

print(t.test(fraud, firearms, conf.level=.95, var.equal = TRUE), 3)

## 
##  Two Sample t-test
## 
## data:  fraud and firearms
## t = -2, df = 18, p-value = 0.03
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -6.824 -0.356
## sample estimates:
## mean of x mean of y 
##      12.1      15.7

To illustate that we will have the same answer when we use the same approach in question 10.2.41

First, we need to get the data from the question

x1 = 12.12
s1 = 3.56
n1 = 10
x2 = 15.71
s2 = 3.32
n2 = 10

---

This is a pooled t-test, to compute pooled sample standard deviation we use the formula \(s_p= \frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}\)

sp = sqrt( ( (n1-1)*s1^2 + (n2-1)*s2^2 )/ (n1+n2-2) )
sp

## [1] 3.442092

We need to find degree of freedom

deg = n1+n2-2

Since the confidence level = 0.95, \(\alpha = 1-.95=.05\)To find \(t_{\alpha/2}\) we run

alpha = .05
t_alpha2 = abs(qt(alpha/2,deg))
t_alpha2

## [1] 2.100922

The 95% confidence interval is from… to…​(Round to three decimal places as​ needed.)

To find confidence interval we use the formular \((\bar x_1 - \bar x_2) \pm t_{\alpha/2}.s_p\sqrt{1/n_1+1/n_2}\)

(x1-x2) - t_alpha2*sp*sqrt(1/n1+1/n2)

## [1] -6.824055

(x1-x2) + t_alpha2*sp*sqrt(1/n1+1/n2)

## [1] -0.3559446

Round to three decimal places

round((x1-x2) - t_alpha2*sp*sqrt(1/n1+1/n2),3)

## [1] -6.824

round((x1-x2) + t_alpha2*sp*sqrt(1/n1+1/n2),3)

## [1] -0.356

We finish a lot of complicated work by using R

---

---

Hope that helps!