10.2.41 pooled t-test right-tailed

Provided below are summary statistics for independent simple random samples from two populations. Use the pooled​ t-test and the pooled​ t-interval procedure to conduct the required hypothesis test and obtain the specified confidence interval.

\(\bar x_{1} = 19, s_1=3, n_1=10\)

\(\bar x_{2} = 17, s_2=4, n_2=15\)

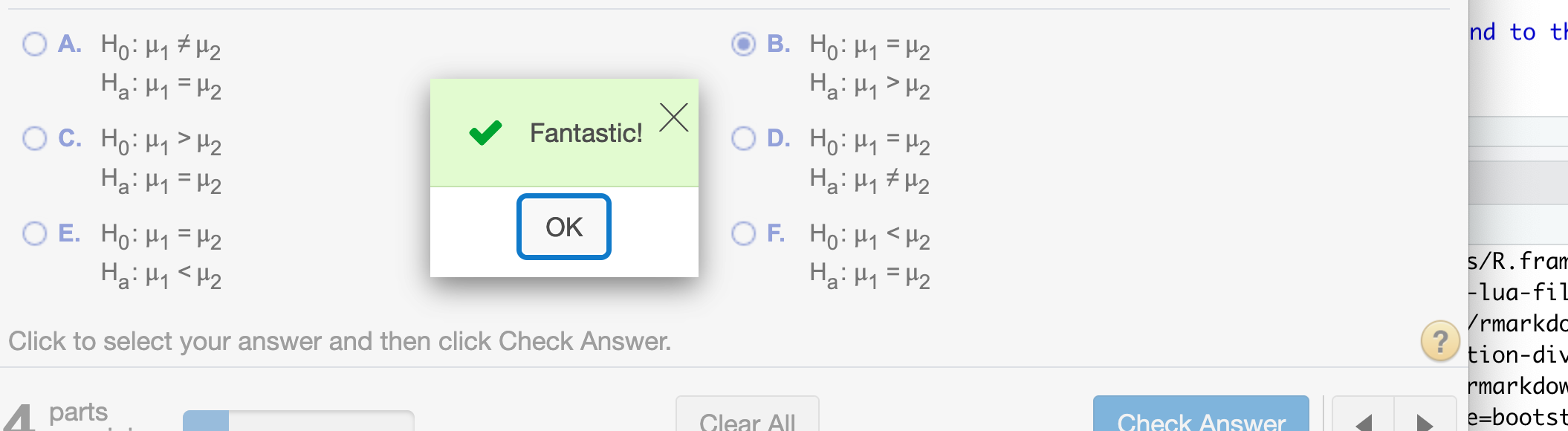
(a).First, what are the correct hypotheses for a right-tailed test?

Since it is a right-tailed test, the correct hypothese is

\(H_0: \mu_1 =\mu_2\)

\(H_a: \mu_1 > \mu_2\)

---

---

Next, compute the test statistic. (Round to three decimal places as​ needed.)

First, we need to get the data from the question

x1 = 19
s1 = 3
n1 = 10
x2 = 17
s2 = 4
n2 = 15

---

This is a pooled t-test, to compute pooled sample standard deviation we use the formula \(s_p= \frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}\)

sp = sqrt( ( (n1-1)*s1^2 + (n2-1)*s2^2 )/ (n1+n2-2) )
sp

## [1] 3.641548

To get the test statistic t we use the formular \(t= \frac{\bar x_1-\bar x_2}{s_p \sqrt{1/n_1+1/n_2}}\), we run

t = (x1-x2)/(sp*sqrt(1/n1+1/n2))
t

## [1] 1.345301

Round the answer to three decimal places

round(t,3)

## [1] 1.345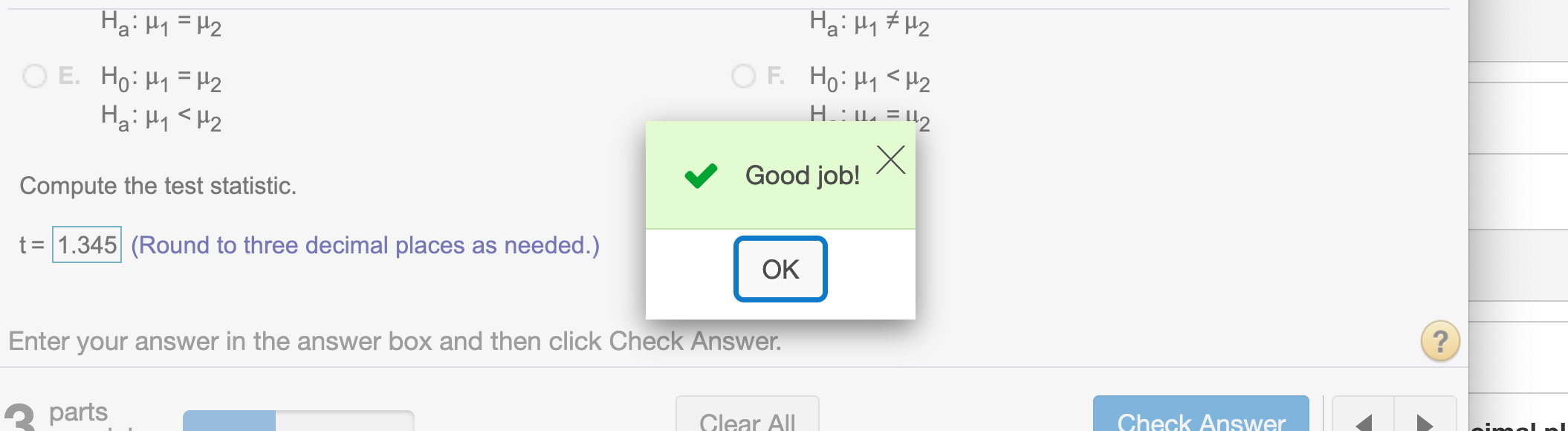

---

---

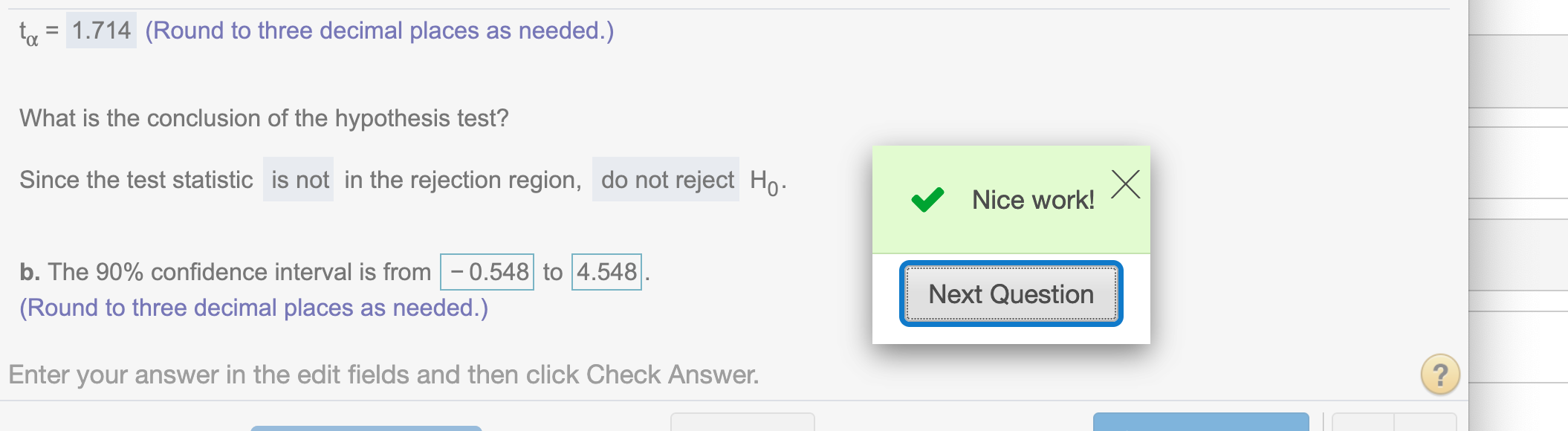
Now determine the critical values. (Round to three decimal places as​ needed.)

We need to find degree of freedom

deg = n1+n2-2

Since this is a right-tailed test and \(\alpha = .01\), the area to the left of alpha is equal to \(1-\alpha\)

alpha = .05
t_critical = abs(qt(1-alpha,deg))
t_critical

## [1] 1.713872

Round the answer to three decimal places

round(t_critical,3)

## [1] 1.714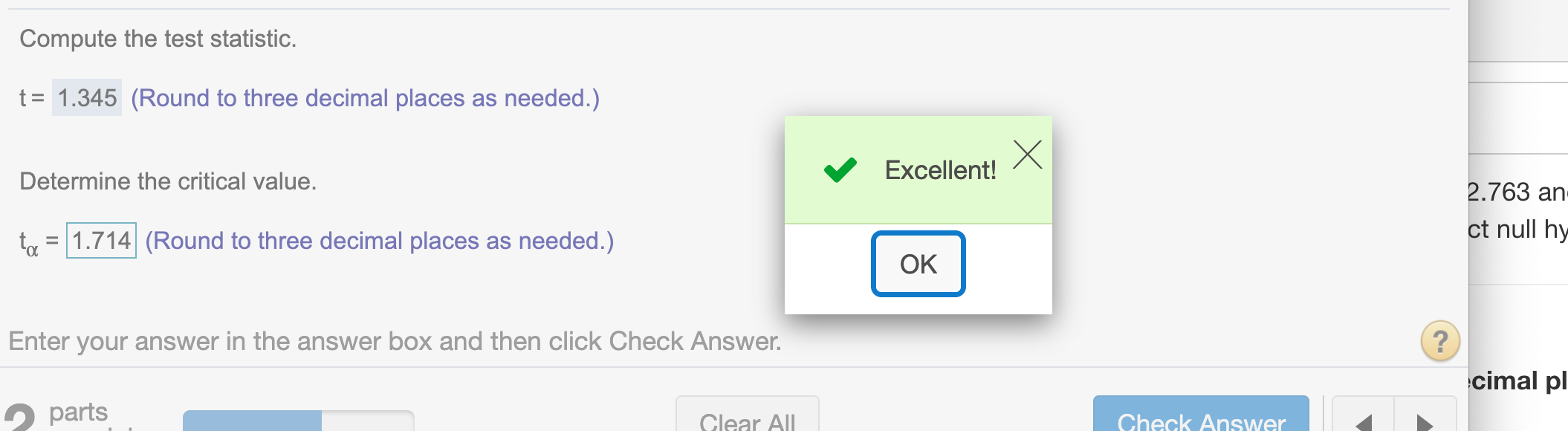

---

---

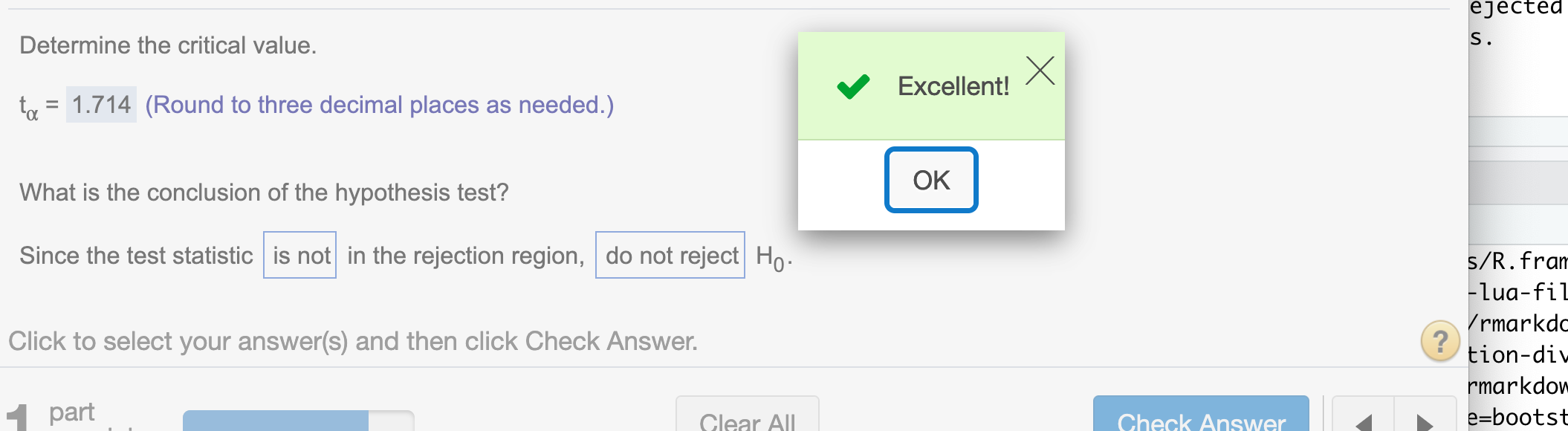
Since our test statistic t = 1.345 < our critical value \(t_{\alpha}\) = 1.714, out test statistic does not lie in the rejected region. So we do not have enough evidence to reject null hypothesis.

---

---

(b) The 90% confidence interval is from… to…​(Round to three decimal places as​ needed.)

90% confidence interval means \(\alpha = .1\) so our critical value \(=\alpha/2=.05\) \(t_{\alpha/2} = t_{critical value}\)

To find confidence interval we use the formular \((\bar x_1 - \bar x_2) \pm t_{\alpha/2}.s_p\sqrt{1/n_1+1/n_2}\)

(x1-x2) - t_critical*sp*sqrt(1/n1+1/n2)

## [1] -0.5479367

(x1-x2) + t_critical*sp*sqrt(1/n1+1/n2)

## [1] 4.547937

Round to three decimal places

round((x1-x2) - t_critical*sp*sqrt(1/n1+1/n2),3)

## [1] -0.548

round((x1-x2) + t_critical*sp*sqrt(1/n1+1/n2),3)

## [1] 4.548

We finish a lot of complicated work by using R

---

---

Hope that helps!