10.5.161 paired t-test with confidence interval
A group of 8 students were given the same standardized test twice to see whether retaking the test affected the score. The table gives the score differences for the 8students. Use the paired t-interval procedure to determine a 95% confidence interval for the difference between the mean scores on the first test and the second test (retake). (Note: \(\bar d = -1.25, s_d = 50.55\))
The 95% confidence interval is from … to …
First, we need to get the data from the question. (We could import the data from Excel)
difference <- c(-30, 30, -40, -40, 80, 60, -50, -20)We can check the data from Note
round(mean(difference),2)## [1] -1.25round(sd(difference),2)## [1] 50.55We have confidence level = .95
First approach use t.test()
t.test(difference, conf.level = .95)##
## One Sample t-test
##
## data: difference
## t = -0.069941, df = 7, p-value = 0.9462
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
## -43.51131 41.01131
## sample estimates:
## mean of x
## -1.25Round to 2 decimal places
print(t.test(difference, conf.level = .95),4)##
## One Sample t-test
##
## data: difference
## t = -0.07, df = 7, p-value = 0.9
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
## -43.51 41.01
## sample estimates:
## mean of x
## -1.25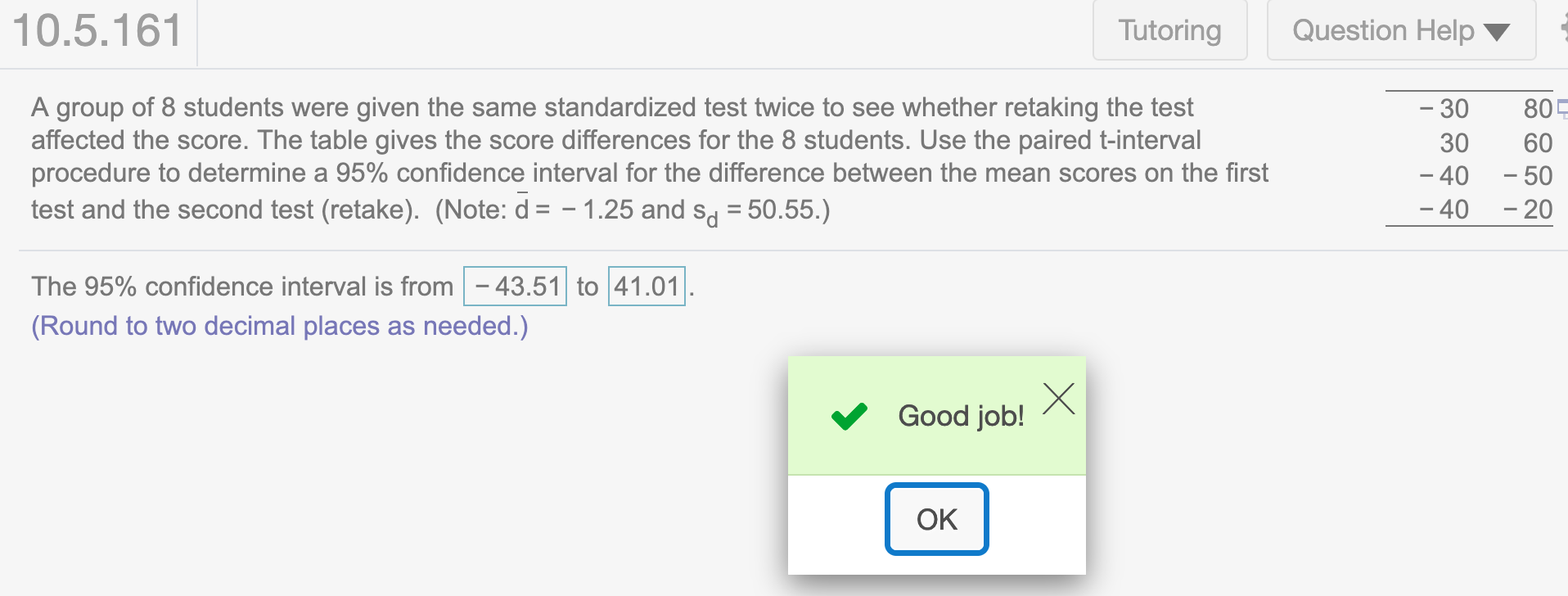
Second appraach to find confidence interval, we can use formula \(\bar d \pm t_{\alpha/2}.\frac{s_d}{\sqrt{n}}\)
Since the confidence level = .95, we have \(\alpha = .05\)
alpha = .05
n = length(difference)
talpha2 = abs(qt(alpha/2, n-1))
mean(difference) + talpha2 *(sd(difference)/sqrt(n))## [1] 41.01131mean(difference) - talpha2 *(sd(difference)/sqrt(n))## [1] -43.51131Round to 2 decimal places
round(mean(difference) + talpha2 *(sd(difference)/sqrt(n)),2)## [1] 41.01round(mean(difference) - talpha2 *(sd(difference)/sqrt(n)),2)## [1] -43.51Hope that helps!