12.1.25 one-proportion z-interval

Given below are the number of successes and sample size for a simple random sample from a population.x = 7​, n = 40​, 90​% level

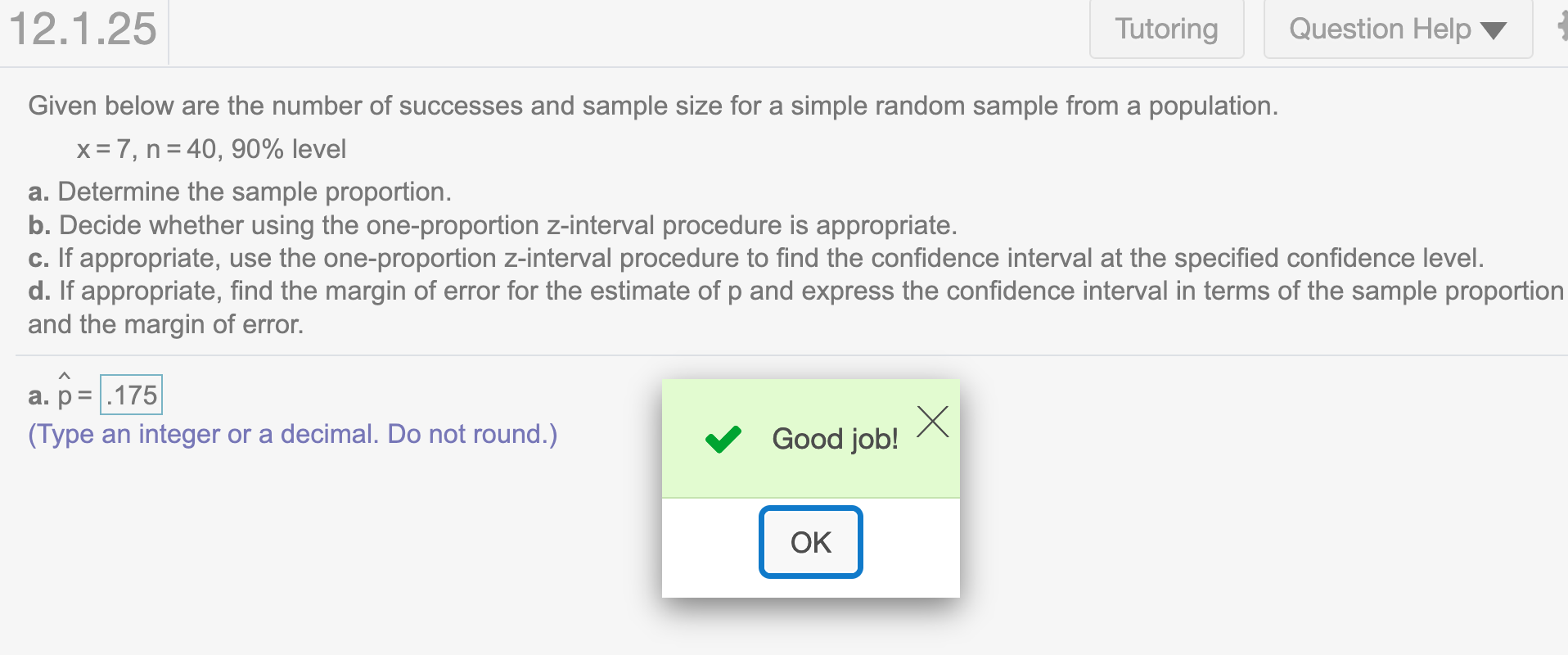
(a). Determine the sample proportion.

x = 7
n = 40
p = x/n
p

## [1] 0.175

\(\hat{p} = .175\)

---

---

(b). Decide whether using the​ one-proportion z-interval procedure is appropriate. There are two conditions for one-proportion z interval:

1. simple random sample

2. x and n-x are 5 are greater

The first condition is passed since the question specifies a simple random sample

To check the second condition we can run

x >= 5

## [1] TRUE

n-x >= 5

## [1] TRUE

---

---

(c). If​ appropriate, use the​ one-proportion z-interval procedure to find the confidence interval at the specified confidence level.

The 90% confidence interval is from … to …

Since confidence level is .9, \(\alpha = 1 - .9 = .1\). So \(\alpha/2=.1/2\)

We can find \(z_{\alpha/2}\) by using qnorm()

alpha = .1
zalpha2= abs(qnorm(alpha/2))

We can find the margin of error for a​ 90% confidence interval by using the formular \(E=z_{\alpha/2}.\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\)

E = zalpha2 * sqrt(p*(1-p)/n)
E

## [1] 0.09881964

Round to three decimal places

round(E, 3)

## [1] 0.099

We can calculate 90% confidence interval by using the formula \(\hat{p} \pm E\)

or we can calculate it directly by using the formula \(\hat{p} \pm z_{\alpha/2}.\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\)

These two formula gives the same answer

p + E

## [1] 0.2738196

p - E

## [1] 0.07618036

Round to three decimal places

round(p + E, 3)

## [1] 0.274

round(p - E, 3)

## [1] 0.076

Second approach: we use direct formula

p + zalpha2 * sqrt(p*(1-p)/n)

## [1] 0.2738196

p - zalpha2 * sqrt(p*(1-p)/n)

## [1] 0.07618036

Round to three decimal places

round(p + zalpha2 * sqrt(p*(1-p)/n), 3)

## [1] 0.274

round(p - zalpha2 * sqrt(p*(1-p)/n), 3)

## [1] 0.076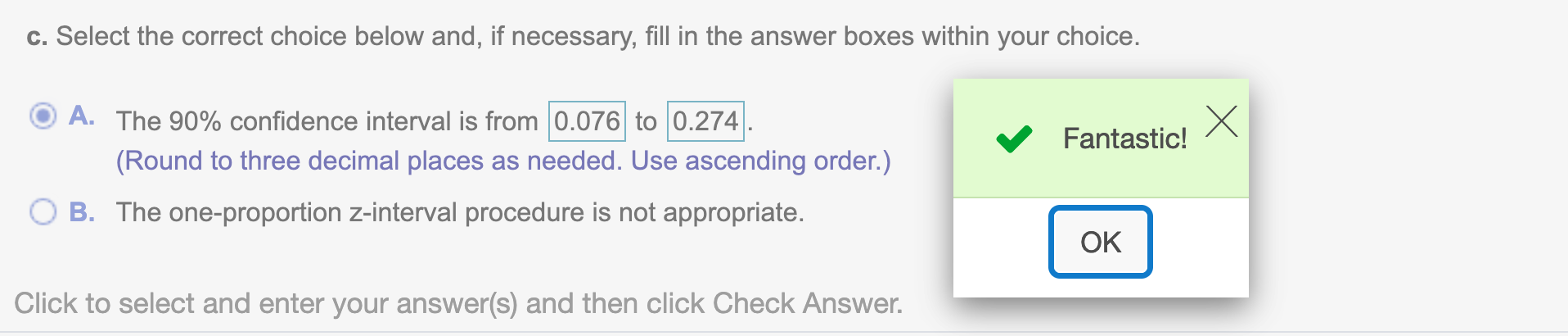

---

---

(d). If​ appropriate, find the margin of error for the estimate of p and express the confidence interval in terms of the sample proportion and the margin of error

If we use the first approach, we already calculate the value of margin of error.

round(E, 3)

## [1] 0.099

If we use the second approach, we have to find the value of margin of error one more time.

---

---

The first approach is nicer and cleaner to use

---

Hope that helps!